CS91 Computer Animation: Lab 3
A room of boxes
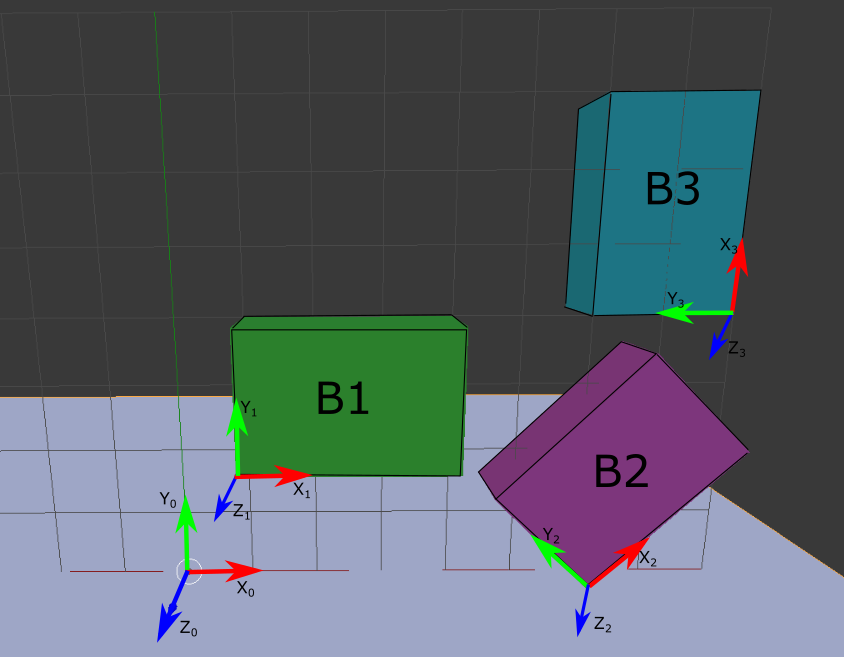
A room has three boxes in it as shown below. Each box has a local coordinate system attached to it. The lengths of all three boxes in the x,y, and z directions of their local coordinate frames are (3,2,1) respectively. The origin of each box is in the lower left-hand corner. The z-axis of each box is aligned with the global Z axis.
The position of B1 with respect to the world (e.g. coordinate system {X0,Y0,Z0}) is p1 = [1 2 1]T.
The position of B2 with respect to the world is p2 = [6 0 0]T.
The position of B3 with respect to the world is p3 = [8 4 0]T.
Furthermore, with respect to the world coordinate system, B2 has been rotated 45 degrees around Z0 and B3 has been rotated 90 degrees around Z0.
It is desired to move B3 to the origin of the world coordinate system and neatly stack box B2 on top of B1.
On a piece of paper, work out the answers of the following questions. Feel free to use tools to check our work or compute numeric values,
such as a calculator, a program such as Octave, or a python script.
- List the frames of reference F10, F20, F30 (in the form of homogeneous matrices) that describe the position and orientations of boxes B1, B2, and B3 with respect to the world.
- How far (e.g. distance) is the origin of box B3 from the origin of the world?
- What is the position of B2 relative to the local coordinate system attached to box B1? Express your answer as a displacement vector.
- What is the homogeneous transformation matrix that stack B2 onto B1?